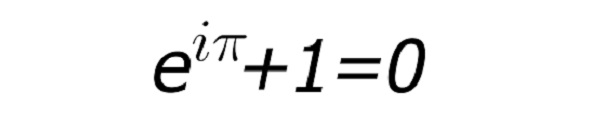Today we refresh our understanding of the discovery and application of the mathematical constant π. The Greek letter π was chosen because it is the first letter of the Greek word “periphery” or “circumference” (περιφέρεια in Greek). It was a natural choice to represent this mathematical constant, which is fundamental to geometry and many other fields of mathematics and science.
Its value was not determined by any one person or organization. Rather, it is a convention that developed over time through the work of many mathematicians; starting with Archimedes. The earliest known use of the symbol π for the ratio of a circle’s circumference to its diameter was by Welsh mathematician William Jones in 1706. However, it was the Swiss mathematician Leonhard Euler who popularized the use of π in the 18th century. Euler used π in his numerous mathematical publications, and his influence helped establish the use of the symbol as standard notation.
e^(i*pi) + 1 = 0
The Euler equation is a mathematical equation that is widely used to analyze the behavior of electrical circuits and to calculate the complex power and reactive power. The complex power of an electrical circuit is a complex number that represents the total power in the circuit, including both the real power (which represents the energy that is actually consumed by the load) and the reactive power (which represents the energy that is stored and released by the circuit’s reactive elements).
The Euler equation is used to represent the complex power in polar form, where the magnitude represents the total power in the circuit, and the phase angle represents the relative contributions of the real and reactive power. By using complex power analysis, engineers can calculate the real power, reactive power, and apparent power (which is the magnitude of the complex power) of the circuit, as well as the power factor, which is the ratio of the real power to the apparent power.
Power factor is an important parameter in AC circuits, as it represents the efficiency with which the circuit is delivering power to the load.
Overall, complex power analysis provides a powerful tool for analyzing the behavior of AC circuits, and it is used extensively in the design and analysis of electrical power systems, shown in the polar form phasor calculation below.

From “Electrical Power System Protection and Coordination” Michael A. Anthony, McGraw-Hill Book Company 1994
Today at 15:00 UTC we will examine this calculation specifically, but also expand upon how the value of π shows up in nearly every other engineering discipline. Use the login credentials at the upper right of our home page.
More:
There are several physical constants that are considered to be important in the known universe. These constants are fundamental properties of nature and do not change over time or space. Here are some of the most important physical constants:
- Speed of light (c): This constant represents the speed at which light travels in a vacuum. Its value is approximately 299,792,458 meters per second. This constant plays a critical role in our understanding of the universe and is the fastest speed that anything can travel in the known universe.
- Planck constant (h): The Planck constant is a fundamental constant of nature that appears in almost all quantum mechanical equations. Its value is approximately 6.626 x 10^-34 joule-seconds. It plays a crucial role in the description of the behavior of subatomic particles and is used in calculations involving quantum mechanics.
- Gravitational constant (G): The gravitational constant represents the strength of the gravitational force between two objects. Its value is approximately 6.674 x 10^-11 newton-meters squared per kilogram squared. This constant plays a crucial role in the study of gravity and is used in calculations involving celestial mechanics.
- Boltzmann constant (k): The Boltzmann constant relates the average kinetic energy of particles in a system to its temperature. Its value is approximately 1.381 x 10^-23 joules per Kelvin. This constant is important in statistical mechanics and is used in calculations involving the behavior of gases, liquids, and solids.
- Avogadro constant (NA): The Avogadro constant represents the number of particles in one mole of a substance. Its value is approximately 6.022 x 10^23 particles per mole. This constant is important in the study of chemistry and is used in calculations involving chemical reactions and the properties of materials.
- Electron charge (e): The electron charge represents the fundamental charge of an electron. Its value is approximately -1.602 x 10^-19 coulombs. This constant is important in the study of electromagnetism and is used in calculations involving electric fields and electric currents.
These constants are critical to our understanding of the universe and are used in a wide variety of fields, from physics and chemistry to engineering and technology.
Happy Birthday!!
Albert Einstein, 14 March 1879 – 18 April 1955.
What else could you say about this great genius?
His works and ideas revolutionized our way of looking at the nature of spacetime. pic.twitter.com/OGljdrrYe8
— Ben Sorowen (@BenSorowen) March 14, 2023