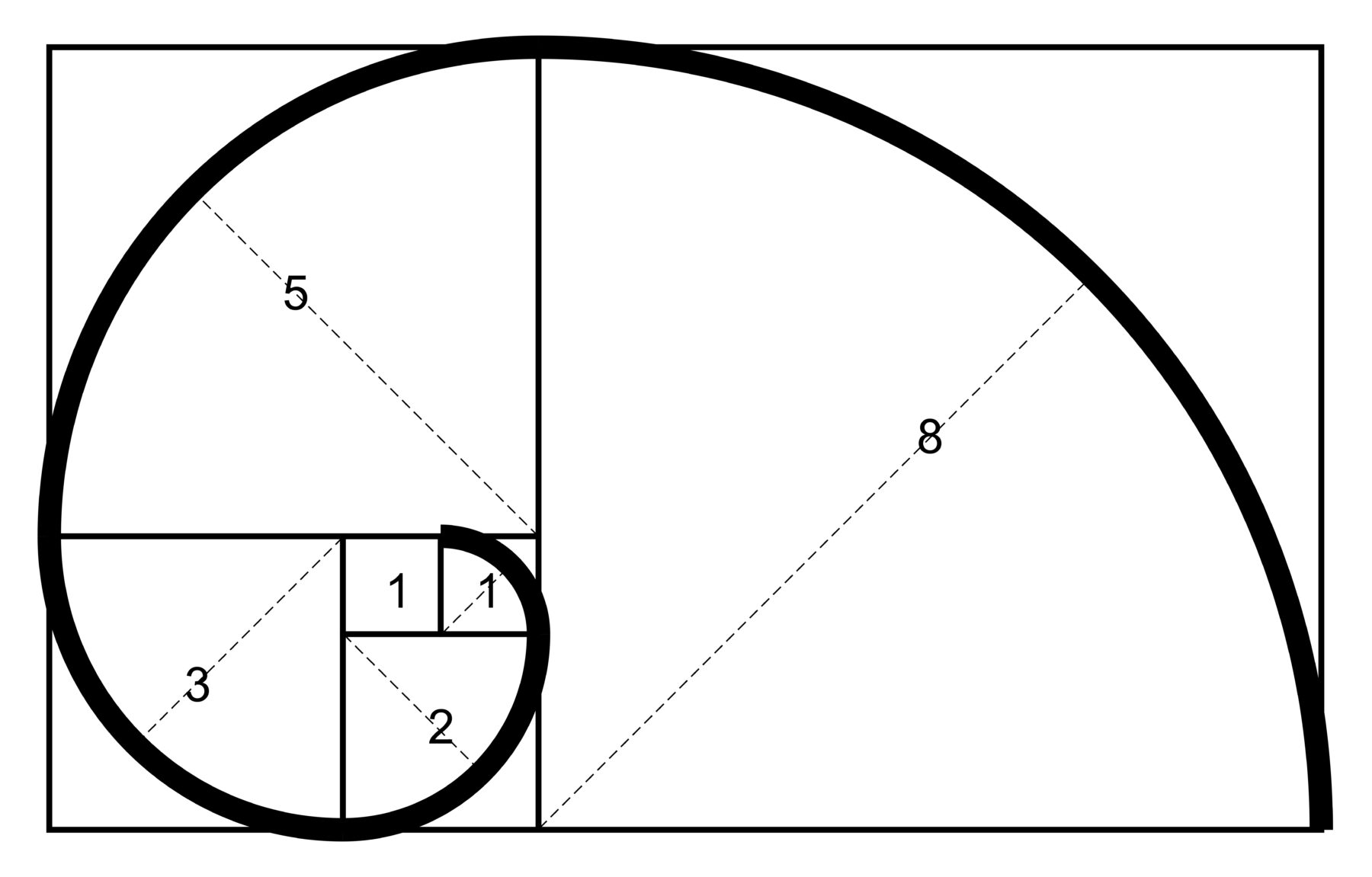
Fibonacci numbers reflect standardization in nature through their consistent appearance in growth patterns and structures, embodying efficient, repeatable designs. These numbers (0, 1, 1, 2, 3, 5, 8, …) govern the arrangement of natural forms, such as the spiral patterns in sunflowers, pinecones, and seashells, where seed or scale counts often match Fibonacci numbers.
This standardization optimizes space and resource distribution, ensuring maximum efficiency—e.g., sunflower seeds pack tightly without gaps. Leaf and branch arrangements (phyllotaxis) follow Fibonacci angles to standardize light exposure and growth. The sequence’s recursive nature mirrors nature’s iterative processes, like branching in trees or cell division, providing a universal template for scalable, stable structures.
The golden ratio, derived from Fibonacci numbers, further standardizes proportions in natural forms, from nautilus shells to galaxy spirals, revealing a mathematical blueprint that unifies diverse biological and physical systems.
Fibonacci numbers find applications in electrical power engineering through their mathematical properties, which can optimize design, analysis, and operation. Here are five applications:
- Power System Network Analysis: Fibonacci sequences can be used in graph theory to model electrical networks. The recursive nature of Fibonacci numbers helps in analyzing hierarchical or layered network structures, such as transmission and distribution grids, to optimize load flow or fault tolerance.
- Transformer Winding Design: The golden ratio, derived from Fibonacci numbers, can guide the geometric arrangement of transformer windings. This helps minimize electromagnetic interference and optimize the efficiency of power transfer by balancing inductance and capacitance.
- Signal Processing for Power Quality: Fibonacci-based algorithms, such as those using the golden section search, are applied in digital signal processing to analyze power quality issues like harmonics or transients. These methods efficiently identify optimal frequency components in noisy power signals.
- Renewable Energy System Optimization: In solar panel or wind turbine array layouts, Fibonacci-inspired spiral patterns (like the golden spiral) can optimize land use and reduce mutual shading or turbulence, improving energy capture efficiency in power generation systems.
- Control System Tuning: Fibonacci numbers can inform the design of control algorithms for power systems, such as in PID controller tuning. The sequence’s recursive properties help in iteratively adjusting parameters to achieve stable and efficient grid operation under varying loads.
These applications leverage the mathematical elegance of Fibonacci numbers to solve practical engineering challenges in power systems.