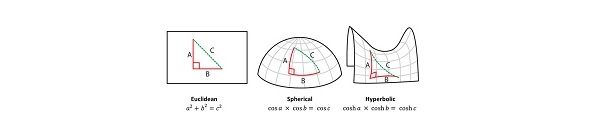
While we reflect upon the fundamental constant π that appears routinely in Euclidean geometry it is also time well spent recognizing other “standard” geometries:
- Hyperbolic geometry: In hyperbolic geometry, the parallel postulate of Euclidean geometry is replaced with a different postulate, which leads to the development of a non-Euclidean geometry. In hyperbolic geometry, the sum of the angles in a triangle is always less than 180 degrees, and there are no parallel lines. This type of geometry has important applications in areas such as non-Euclidean geometry, topology, and physics.
- Elliptic geometry: In elliptic geometry, the parallel postulate is replaced with a different postulate that leads to the development of a non-Euclidean geometry. In elliptic geometry, the sum of the angles in a triangle is always greater than 180 degrees, and there are no parallel lines. This type of geometry has important applications in areas such as geometry, topology, and cartography.
- Projective geometry: Projective geometry is a type of geometry that studies properties that are invariant under projective transformations. It is used extensively in areas such as computer graphics, computer vision, and machine learning, as well as in the study of complex projective structures in algebraic geometry.
Each of these geometries has its own set of axioms, theorems, and properties that are distinct from those of Euclidean geometry. They have important applications in a wide range of fields, including mathematics, physics, engineering, computer science, and many others.
Understanding non-Euclidean geometries is important for several reasons:
- Broadening our understanding of geometry: Non-Euclidean geometries expand our understanding of geometry beyond the traditional Euclidean model, which is limited to two-dimensional and three-dimensional space. Non-Euclidean geometries allow for the exploration of curved spaces, which can have practical applications in fields like physics, engineering, and computer graphics.
- Advancing scientific knowledge: Non-Euclidean geometries have played a crucial role in the development of modern physics, particularly in the study of gravity and the structure of the universe. For example, Einstein’s theory of general relativity relies heavily on non-Euclidean geometries to explain the behavior of massive objects in the presence of gravity.
- Challenging our assumptions: Non-Euclidean geometries challenge our assumptions about the nature of space and our perceptions of reality. By exploring these alternative models of space, we can gain a deeper understanding of the limits of our knowledge and the nature of the universe.
- Encouraging creativity and innovation: Exploring non-Euclidean geometries can stimulate creativity and innovation in fields like art, architecture, and design. By breaking free from traditional Euclidean constraints, designers can create novel and innovative structures that challenge our perceptions of space and form.
Understanding non-Euclidean geometries is important for expanding our knowledge of the universe, challenging our assumptions, and encouraging creativity and innovation in various fields.