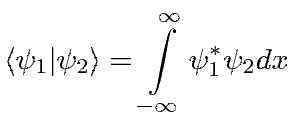Quantum Computing for High-School Students: An Experience Report

Quantum Computing for High-School Students An Experience Report

Prashanti Priya Angara, et. al

Department of Computer Science, University of Victoria, Victoria, Canada

Abstract: Quantum computing is an emerging field that can revolutionize our ability to solve problems and enable breakthroughs in many areas including optimization, machine learning, chemistry, and drug design. With the increasing computational power of quantum computers and the proliferation of quantum development kits, the demand for a skilled workforce in quantum computing increases significantly. The theory of quantum computing lies at the crossroads of quantum physics, mathematics, and computer science. The field of quantum computing has matured and can now be explored by all students. While today, quantum computers and simulators are readily accessible and programmable over the internet, quantum computing education is just ramping up.

This paper describes our experiences in organizing and delivering quantum computing workshops for high-school students with little or no experience in the abovementioned fields. We introduce students to the world of quantum computing in innovative ways, such as newly designed “unplugged” activities for teaching basic quantum computing concepts. Overall, we take a programmatic approach and introduce students to the IBM Q Experience using Qiskit and Jupyter notebooks. Our experiences and findings suggest that basic quantum computing concepts are palatable for high-school students, and-due to significant differences between classical and quantum computing-early exposure to quantum computing is a valuable addition to the set of problem-solving and computing skills that high-schoolers obtain before entering university.

Dirac Bra-Ket notation, also known simply as bra-ket notation, is a standard mathematical notation used extensively in quantum mechanics and quantum computing. It was introduced by Paul Dirac and provides a convenient and powerful framework for describing quantum states and their evolution. Here are several ways in which Dirac Bra-Ket notation is important in quantum computing:

1. Representation of Quantum States:
   • Kets (|ψ⟩): Quantum states are typically represented as kets, denoted by |ψ⟩. This notation simplifies the representation of complex vectors in a Hilbert space.
   • Bras (⟨ψ|): The corresponding dual vectors, or bras, are denoted by ⟨ψ|. These are the complex conjugate transpose of the kets.
2. Inner Product:
   • The inner product of two states |ψ⟩ and |φ⟩ is written as ⟨ψ|φ⟩. This notation succinctly captures the concept of the probability amplitude, which is fundamental to quantum mechanics and quantum computing.
3. Outer Product:
   • The outer product, written as |ψ⟩⟨φ|, represents a linear operator that can be used to construct projection operators and density matrices, which are crucial in quantum algorithms and quantum information theory.
4. Operators and Measurements:
   • Quantum operators, such as Hamiltonians and measurement operators, can be conveniently expressed using bra-ket notation. For example, an operator A^\hat{A}A^ acting on a state |ψ⟩ can be written as A^∣ψ⟩\hat{A}|ψ⟩A^∣ψ⟩.
   • Measurement probabilities are often expressed in terms of bras and kets, e.g., the probability of measuring a state |ψ⟩ in the basis state |φ⟩ is |⟨φ|ψ⟩|².
5. Tensor Products:
   • In quantum computing, systems are often composed of multiple qubits, which are represented by tensor products of individual qubit states. Bra-ket notation elegantly handles these tensor products, e.g., |ψ⟩⊗|φ⟩.
6. Quantum Gates and Circuits:
   • Quantum gates, which perform operations on qubits, can be represented using unitary operators in bra-ket notation. For example, the action of a gate U on a qubit state |ψ⟩ is written as U|ψ⟩.
7. Simplifying Complex Expressions:
   • Bra-ket notation simplifies the manipulation of complex expressions involving quantum states and operators, making it easier to derive results and understand the behavior of quantum systems.
8. Formalism for Quantum Algorithms:
   • Many quantum algorithms, such as the Quantum Fourier Transform (QFT) and Grover’s search algorithm, are conveniently expressed and analyzed using bra-ket notation, providing clarity and insight into their functioning.

In summary, Dirac Bra-Ket notation is essential in quantum computing for its ability to provide a clear and concise way to describe and manipulate quantum states, operators, and the evolution of quantum systems. It is a powerful tool that underpins much of the theory and practice in the field.